Бутылка Клейна. Невозможное. Оптические иллюзии и обманы зрения. Интеллектуальные развлечения.

E-mail:
Пароль:
	Запомнить
	Войти
	Амнезия? Я новичок

Бутылка Клейна

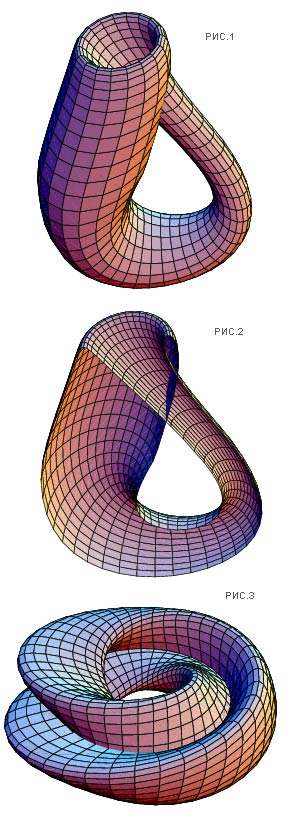
В математике Бутылка Клейна (рис.1.) — это определённая неориентируемая поверхность рода 1, т. е. поверхность (двумерное топологическое пространство), у которой нет различия между внутренней и внешней сторонами. Бутылка Клейна впервые была описана в 1882 г. немецким математиком Ф. Клейном. Она тесно связана с лентой Мёбиуса и вложениями проективной плоскости, например поверхностью Боя.

Чтобы сделать бутылку Клейна, необходимо взять бутылку с отверстием в донышке, вытянуть горлышко, изогнуть его вниз, и продев его через отверстие в стенке бутылки (для настоящей бутылки Клейна в четырёхмерном пространстве это отверстие не нужно, но без него нельзя обойтись в трёхмерном евклидовом пространстве), присоединить к отверстию на дне бутылки.

В отличие от обыкновенного стакана у этого объекта нет «края», где бы поверхность резко заканчивалась. В отличие от воздушного шара можно пройти путь изнутри наружу не пересекая поверхность (т. е. на самом деле у этого объекта нет «внутри» и нет «снаружи»).

Название, по-видимому, происходит от неправильного перевода немецкого слова Flache (поверхность), которое в немецком языке близко по написанию к слову Flasche (бутылка).

При рассечении бутылки Клейна получается лента Мёбиуса (рис.2). На рис.3 представлена развертка бутылки Клейна.