Красота математических поверхностей

Все, разумеется, строили в школе графики, до невозможности проклиная училку по геометрии. Так вот, если кто-то помнит, то впервые с понятиями бесконечности в изображении графиков фукнций народ столкнулся ещё там, когда описывался простейший график в виде прямой, бесконечной по протяженности. Следом за ней пошла гипербола - график функции y = 1/x, бесконечно приближающаяся к осям координат.
Но мозгу здорового человека довольно трудно представить себе график, который состоит из бесконечности, пронизывая всё пространство на плоскости, и рисунок которого можно увеличивать без остановки.
В математике есть такие графики, называются они фракталами.
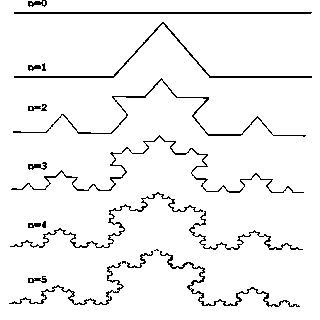
Описать структуру фрактала можно на примере береговой линии: издали она имеет вид кривой, однако при приближении у кривой появляются другие неровности, и сколько не приближай взгляд, кривая никак не исчезает. На той же основе и были созданы фрактальные графики. Вчастности, на рисунке слева приведен пример кривой Коха, самой простой из всех фрактальных функций.
Слово фрактал образовано от латинского fractus и в переводе означает "состоящий из фрагментов". Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
Фракталы бывают нескольких типов
Самые простые из них - геометрические, как кривая Коха. Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.
Рассмотрим один из таких фрактальных объектов - триадную кривую Кох [3]. Построение кривой начинается с отрезка единичной длины (рис. кривой Коха) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На примере было изображено пятое поколение кривой. При функции, где n>?, изображение начинает уходить в ту степь, куда не ступала нога человека: в бесконечность.
Самая крупная группа фракталов - алгебраические.
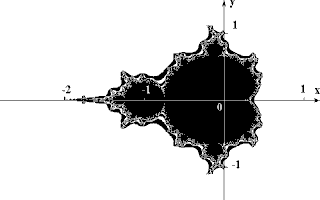
Самое известное из них - множество Мандельборта, самое красивое из всего, созданного точными науками. Если кому-то что-то это скажет, формула множества Мандельброта записывается так: Z[i+1] = Z[i] * Z[i] + C, где Zi и C - комплексные переменные. Итерации выполняются для каждой стартовой точки C прямоугольной или квадратной области - подмножестве комплексной плоскости. Итерационный процесс продолжается до тех пор, пока Z[i] не выйдет за пределы окружности радиуса 2, центр которой лежит в точке (0,0), (это означает, что аттрактор динамической системы находится в бесконечности), или после достаточно большого числа итераций (например 200-500) Z[i] сойдется к какой-нибудь точке окружности. В зависимости от количества итераций, в течении которых Z[i] оставалась внутри окружности, можно установить цвет точки C (если Z[i] остается внутри окружности в течение достаточно большого количества итераций, итерационный процесс прекращается и эта точка растра окрашивается в черный цвет).
Вышеописанный алгоритм дает приближение к так называемому множеству Мандельброта. Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки имеющие черный цвет). Точки принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
ХОРОШО, ХОРОШО!!! Я понимаю, тошнит уже от науки. Не волнуйтесь, сейчас будет и красота. Вот, взгляниет на множество Мандельборта в натуре, увеличение в 0 раз:

А ВОТ СЕЙЧАС НАЧНЁТСЯ ВОЛШЕБСТВО
Фракталы очень просто строить самому, задав конечный предел интеграции. Для этого сейчас специально пишут программы, в зависимости от желаний можно создать самые различные изображения, цветные, непонятные, шокирующие. Вот, например, несколько вариаций того же множества:

А вот версия Мандельброта, если график разместить в трёхмерном пространстве:

И не стоит думать, что там, где изображения не видно, око якобы кончается. Напротив: оно продолжается везде, нужно тлько правильно задатьпредел интеграции и иметь достаточно мощный микроскоп. Но при любом увеличении всегда можно сказать, что множество находится везде и нигде одновременно.
А вот область множества Мандельброта, увеличенная в несколько тысяч раз (!).

Вот еще несколько рисунков фрактальных поверхностей



Посмотреть фрактальные поверхности в анимации (и убедиться, что фрактал бесконечный) можно на сайте images.beggerlybend.com (открывается в новом окне)
А на сайте www.ocf.berkeley.edu вы найдете алгоритмы и формулы для самостоятельного построения поверхностей.
Dmitry 19.04.2005




10 комментариев (в архиве — 17 комментариев)
svzuvszbgtz (0)
25.08.2011 13:30
99l5zK unuiwzprcnfd
awckjynf (0)
18.08.2011 21:27
GE8DYU kxlutklrvogv
Wilhelmina (0)
18.08.2011 11:56
I thuoght finding this would be so arduous but it's a breeze!
Альфия (0)
15.03.2011 04:33
Каков практический смысл изучения фракталов?
Виктор Карпов (0)
17.01.2011 01:01
По-моему, трехмерные фракталы не такие красивые, как двумерные — не понятно только почему.
StaticTime (0)
16.11.2010 03:15
Всегда любила математику=)) Одна из самых замечательных наук,как и физика=) Данный обзор только подтверждает ее величие
я (0)
07.03.2010 12:13
А Я ВИДЕЛА ФИЛЬМ ПРО ФРАКТАЛЫ.ТАМ ЧЁТ ГОВОРИЛИ,ЧТО НА ИЗУЧЕНИЕ ОДНОГО ФРАКТАЛА МОЖЕТ УЙТИ МИЛЛИОНЫ ЛЕТ!
Сергей32 (-78)
11.03.2011 19:50
я: Фрактал невозможно изучить до конца. Он - бесконечность)
Виктор Карпов (0)
17.01.2011 01:03
я: Эмм.. Что это за фильм? Кстати, есть отличный фильм, по-моему, называется «Множество Мандельброта и Сознание», в тему к необычному применению фракталов и там где они используются. Аннотация: «Каждый фрактал разбивается на бесконечно малые частицы, но при это всегда будет отражать все целое…Когда один фрактал меняет свой узор общая суммарность всего узора меняется вместе с ним… Это иллюстрирует что не нужно пробуждать весь мир.. Нужно изменить себя!»
фы (1)
14.12.2009 22:17
ыыы