Неоднозначные, парадоксальные и неопределенные фигуры. Иллюзии. Познавательные статьи и необычные фотографии.

E-mail:
Пароль:
	Запомнить
	Войти
	Амнезия? Я новичок

Неоднозначные, парадоксальные и неопределенные фигуры

Продолжаем публикацию книги Р. Л. Грегори "Разумный глаз: Неоднозначные фигуры" (Продолжение)

В предыдущей публикации мы упоминали два вида неоднозначности: во-первых, неоднозначность глубины на рисунках (проекциях куба) и, во-вторых, неоднозначность содержания рисунков (портрет молодой леди — старой ведьмы). Так как оба вида перцептивной неоднозначности существенно различаются, им следует дать свои названия: «глубинная неоднозначность» и «неоднозначность содержания». Перейдем теперь к планированию экспериментов для дальнейшего изучения этих феноменов, но тут необходимо учесть, что в обоих случаях потребуются совершенно разные эксперименты.

Для изучения глубинной неоднозначности, с которой мы начнем, нужен простейший аппарат; заинтересовавшийся читатель легко может изготовить его сам. Результаты опытов многообещающи, и можно рассчитывать на то, что они помогут ответить на основной вопрос: как происходит зрительное восприятие объектов? При этом следует помнить, что внезапные изменения восприятия могут происходить и в тех ситуациях, когда изображение на сетчатке глаза остается неизменным. Это позволяет, сохраняя постоянство изображения, исследовать происходящие в мозгу центральные процессы принятия решений, и особенно то, как на основе сенсорных данных избираются перцептивные гипотезы, то есть альтернативы восприятия. Именно этот вопрос мы считаем здесь основным, центральным. Куб Неккера лишен перспективы; его грани точно равны по размеру и по форме, тем не менее в любой данный момент одна из них воспринимается как передняя, а другая — как задняя грань куба. На рисунке куба, выполненном с соблюдением перспективы, одна (передняя) грань куба больше другой (задней). Такая разница в размерах служит сигналом глубины; мы можем предположить, что введение перспективы в рисунок помешает кубу «перевертываться», поскольку разница в размерах должна улучшить неоднозначность фигуры. Проведя опыт и зарегистрировав число, показывающее, сколько раз в течение определенного отрезка времени (порядка нескольких минут) произошло перевертывание куба, мы установим влияние перспективы (или любого другого фактора, влияющего на неоднозначность фигуры). Из опыта видно, что перевертывание по глубине — лишь один из нескольких наблюдаемых весьма любопытных эффектов. Прочие эффекты, обнаруживаемые нами в этих экспериментах, показывают разницу между тем, как мозг обращается с картинами и как — с объектами.

Кроме исследования влияния перспективы, мы попытаемся также выявить влияние включения второго глаза, то есть влияние стереоскопически воспринимаемой глубины. Посмотрим еще, к чему приведет дополнительный фактор — движение. И наконец, сравним восприятие нескольких разных картин с непосредственным восприятием объекта, изображенного на этих картинах.

Чтобы провести эти эксперименты, необходима методика, позволяющая по-разному изображать объекты; придется давать картины с перспективой, «дозируя» последнюю от нуля до максимума; понадобятся также трехмерные картины, выполняемые с применением стереоскопической техники. Все это достаточно просто удается, если использовать тени. Воспользуемся чуть усложненной схемой теневой проекции. Теневой проектор может давать любую перспективу (в том числе и нулевую); он же может дать двойное изображение, вполне достаточное для стереоскопического восприятия. Сам аппарат весьма прост. Это маленький «точечный» источник света, отбрасывающий тень предмета на матовый экран; в качестве предмета можно использовать, к примеру, каркасный куб. Глаз увидит на экране плоское изображение предмета. Оно будет иметь перспективу, выраженную тем сильнее, чем меньше расстояние между источником света и объектом; перспектива здесь будет зависеть только от расстояния. Если бы оно было бесконечно большим, перспективы не было бы совсем. Вместо того чтобы брать очень большие расстояния, используем большое параболическое зеркало: оно позволит нам сделать пучок падающих на экран лучей света параллельным. Источник света при этом поместим в фокусе параболического зеркала, а объект — в любой точке оси от центра зеркала к центру экрана; объекту можно даже придать постоянное вращение — и тогда у нас будет непрерывно меняющееся изображение.

Чтобы получить стереоизображение нашего предмета, добавим еще один «точечный» источник света. Оба источника поместим рядом так, чтобы расстояние между осями объектов было примерно равно расстоянию между глазами человека (около 60 миллиметров). Это позволит дать на экран две плоские проекции объекта — по одной для каждого глаза наблюдателя. Обе они будут различаться между собой точно так же, как различаются в норме ретинальные изображения обычного объекта в обоих глазах наблюдателя. Таким образом, мы получим правильно спроециро ванную пару картин — стереопару изображений объекта.

Неоднозначные, парадоксальные и неопределенные фигуры : Рис.1
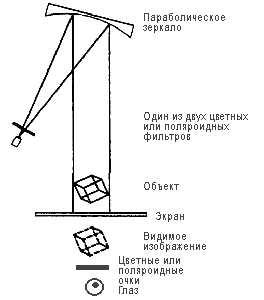
Можно скомбинировать проекцию из пары источников (здесь показан только один) для получения стереоизображения с отражением от параболического зеркала — для устранения перспективы. Тогда образ предмета будет объемным, но не перспективным. Такой образ, невозможный в реальной жизни, исключительно полезен для целей нашего эксперимента

Осталось лишь устроить так, чтобы правый глаз получил свою картинку, а левый — свою. Каждую картинку следует сделать видимой только для одного глаза. Это достигается с помощью фильтров — поляроидных либо цветных. Пусть теперь наблюдатель смотрит на экран сквозь очки, в которых правое стекло красное, а левое зеленое; тогда каждый глаз получит «свою» проекцию объекта. В мозгу обе «проекции» сольются и возникнет стереоскопический образ объекта. Наблюдатель воспримет этот образ как трехмерную пространственную фигуру. Прием двойной проекции, позволяющий нам работать обоими глазами и получать при этом стереоэффект, особенно важен при изучении незнакомых предметов.

Сравним теперь то, что получается, когда мы рассматриваем предмет непосредственно, с тем, что мы видим, воспринимая его на картине, при каждом из четырех видов проекции. Несмотря на то что перспективу можно в принципе менять плавно, мы будем пользоваться только двумя ее вариантами:

перспектива при малом расстоянии между источником света и объектом;
нулевая перспектива — при проекции объекта из оптической бесконечности.

Для сравнения возьмем только два предмета: каркасный куб и усеченную пирамиду.

Неоднозначные, парадоксальные и неопределенные фигуры : Рис.2
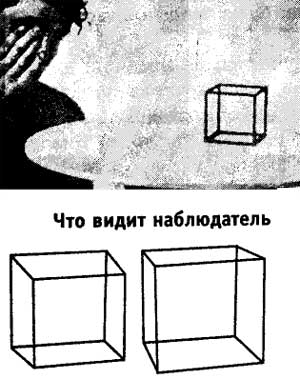
Наблюдатель смотрит одним глазом. Восприятие объекта. Куб воспринимается как куб. В глазу изображение дальней грани меньше по размеру, но при этом она не выглядит уменьшенной. Все углы имеют вид прямых (хотя в ретинальном изображении на дне глаза они не являются таковыми, потому что ретинальное изображение есть перспективная проекция предмета). Когда куб переворачивается в глубину, подобно тому как это происходит с кубом Неккера, он уже больше не выглядит как куб. Та грань, что кажется более удаленной, выглядит сильно увеличенной, а грань, воспринимаемая впереди, кажется уменьшенной. Воспринимается не куб, а усеченная пирамида. Это изменение видимой формы предмета происходит каждый раз совершенно внезапно и одинаково у всех наблюдателей

Наблюдатель смотрит одним глазом. Монокулярная перспектива. Восприятие картины. Изображение куба, точно выполненное в перспективной проекции на плоскости листа, выглядит искаженным: одна грань меньше другой, противоположной. Меньшая грань кажется дальней гранью куба, но в то же время видно, что она находится в плоскости листа на том же расстоянии от наблюдателя, что и большая (передняя) грань. Глубина здесь парадоксальна: видимая фигура представляет собой и объемный куб, и плоское изображение. При перцептивном перевертывании фигура не меняет формы в отличие от куба, наблюдаемого в натуре

Наблюдатель смотрит одним глазом. Монокулярная нулевая перспектива. Восприятие объекта. Каркасный куб заменен усеченной пирамидой, которая обращена к глазу наблюдателя меньшей по размеру гранью. При этом мы выбрали такое расстояние, что на ретине глаза изображение объективно меньшей грани имеет точно ту же величину, что и изображение объективно большей грани. (Объект устанавливают так: находят то положение и расстояние, при которых ближняя грань точно закрывает дальнюю; затем слегка его поворачивают, чтобы дальняя грань была видна.) Объект не выглядит как куб. Дальняя грань кажется больше ближней. При перцептивном перевертывании большей кажется та грань, которая воспринимается как дальняя. Таким образом, объект все время выглядит как усеченная пирамида, но большей кажется то одна, то другая грань — та, которая выглядит в данный момент более удаленной

Наблюдатель смотрит одним глазом. Восприятие картины. На картине куб Неккера. Перспектива не дана: размеры «ближней» и «дальней» граней куба одинаковы. Они и воспринимаются как одинаковые при обоих вариантах перцептивного перевертывания фигуры. (Обратите внимание, однако, на последующие замечания о важности фактуры плоского листа.) Глубина здесь парадоксальна

Наблюдатель смотрит двумя глазами. Стереоперспектива. Восприятие объекта. Каркасный куб воспринимается как куб. Все ребра одинаковой длины, все углы прямые, несмотря на то что в ретинальном изображении каждого глаза дальняя грань куба отражена меньшей по размеру, чем ближняя грань. Перцептивное перевертывание куба случается редко, но оно, безусловно, может происходить. «Вывернутый наизнанку» куб кажется не вполне реальным, искаженным, форма его нарушается подобно тому, как это происходит при наблюдении одним глазом; в частности, грань, которая кажется дальней, выглядит сильно увеличенной

Наблюдатель смотрит двумя глазами. Стереоперспектива. Восприятие картины. Картина кажется совершенно объемной, нарисованный объект выглядит удивительно реальным — до того, что трудно отличить его от такого же, но «настоящего» каркасного куба, наблюдаемого в натуре. Видимый куб не имеет искажения формы. Иногда (редко) он перевертывается — и тогда стереокартина выглядит искаженной точно так же, как в случае перцептивного перевертывания реального каркасного куба

Наблюдатель смотрит двумя глазами. Стереонулевая перспектива. Восприятие объекта. Усеченная пирамида выглядит именно как усеченная пирамида: ближняя грань меньше дальней, как это и есть в действительности, хотя и та, и другая грани дают в обоих глазах одинаковые по величине изображения. При перцептивном перевертывании (что случается редко) грань, кажущаяся более удаленной, выглядит увеличенной

Наблюдатель смотрит двумя глазами. Стереонулевая перспектива. Восприятие картины. Физически ближняя и дальняя грани куба изображены в плоскости листа одинаковыми по размеру, но выглядят они различно: грань, которая воспринимается как дальняя, кажется увеличенной. Увеличенной она кажется и при перцептивном перевертывании (что случается редко), но при этом вся объемная фигура принимает странный, как бы нереальный вид

Условия, в которых происходит (да) либо не происходит (нет) искажение. Под «искажением» мы понимаем тот случай, когда фигура не выглядит похожей на куб. Под «парадоксальностью» мы подразумеваем тот случай, когда на глубинное расположение деталей фигуры влияет фон: фигура как бы лежит в плоскости фона и в то же время в квазиглубинном пространстве монокулярного зрения. (Этот парадокс глубины фигуры не имеет места ни при прямом наблюдении предметов, ни при стереовосприятии картин.)

Глубина воспринимается правильно
Монокулярная перспектива		Монокулярная нулевая перспектива	Стереоперспектива	Стереонулевая перспектива
Предмет	Нет	Да	Нет	Нет (обычно)
Картина	Нет? (парадоксально)	Да (парадоксально)	Нет	Да
Глубина воспринимается навыворот
Предмет	Да	Да	Да (редко)	Да (редко)
Картина	Да? (парадоксально)	Да (парадоксально)	Да (редко)	Да (редко)

Наши опыты показали также, что картины могут быть удивительно мало пригодны для опознания даже знакомых предметов. Таблица, в которую сводятся основные наблюдения, позволяет увидеть, что происходит с каждой из четырех проекций в тех случаях, когда фигура воспринимается правильно, и в тех случаях, когда она вывернута по глубине наизнанку. Что говорят о восприятии проведенные нами опыты? Многое, и в том числе то, что зрительное восприятие картин очень отличается от зрительного восприятия обычных, «нормальных» объектов. А это значит, что картины не являются нормальными предметами для глаз, они представляют совершенно особый случай восприятия. И поскольку большинство экспериментов по восприятию проводилось с помощью картин, следует очень осторожно оценивать результаты таких экспериментов, особенно что касается перенесения выводов, сделанных в экспериментах с картинами, на восприятие нормальных объектов.

Далее в выпусках: