Трогаем бесконечность. Мебиус, Клейн и другие топологические парадоксы
Односторонние поверхности : Лист Мебиуса и Бутылка Клейна
Мы так часто слышим слово – Бесконечность, а не хотелось ли вам когда ни будь подержать эту самую бесконечность в своих руках? Для того что бы сделать это вам придётся взять в руки бумагу, ножницы и клей. Отрежьте полоску бумаги и склейте её как показано на рисунке.
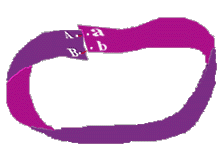
У Вас получилась такая односторонняя поверхность:

Кольцо Мебиуса
Что значит односторонняя? Это значит, что муравей (или житель Плоскатии , о котором мы говорили в предыдущей статье) побывает на обеих сторонах этого листа не переходя через край. Это значит, что вы можете не отрывая карандаша от бумаги, и не переходя через край закрасить эту фигуру с обеих сторон.

Если вам кажется что ничего особенного в этом нет, тогда попробуйте решить следующую головоломку:
Это древняя головоломка о трёх колодцах и трёх домах.
В ряд стоят 3 дома, напротив каждого из них есть по колодцу. Нужно от каждого дома сделать тропинки к каждому из колодцев так, что бы никакие 2 тропинки не пересекались.
Ниже вы можете сделать это в динамике, только колодцы тут заменены: Газом, Водой и Электричеством. Нужно к каждому из домов провести и газ и воду и электричество, и что бы ни какие 2 трубы ( электрические кабеля) не пересекались.
Ну как? Не получается?
Не так давно была доказана неразрешимость этой задачи при помощи формулы Эйлера (см. заметку на нашем сайте "Прогулка по мостам").
Но задача эта не разрешима на ПЛОСКОСТИ, НА БУМАГЕ.
Разве мы с вами живем на бумаге? Нас со школы учили оперировать понятиями «Эвклидовой геометрией», а по простому - нас со школы учили мыслить «Плоско». Что же касается этой головоломки, то она имеет решение, только не в придуманном, а в реальном мире. В этом нам поможет Лист Мебиуса. Соедините соответствующие буквы, и получите ответ на головоломку.

Разумеется, это только начало. Лист Мебиуса таит в себе ещё много неожиданностей.
Фокус №1
Сделайте ещё один Лист Мебиуса, повёрнутый на пол оборота (180 градусов). А теперь попробуйте его разрезать посредине.

Я Вам не скажу что получится так как:
а) Если Вы уже держите в руках Лист Мебиуса и ножницы, то лишить Вас удовольствия наблюдать за тем, что произойдёт после разрезания – это просто преступление.
б) Если Вы и не думали брать в руки ножницы – тогда сказанный мною результат вас не удивит.
Ну как получилось? Обратите внимание, на сколько оборотов закручен полученный экземпляр?
Фокус №2
Закрутите Лист на 2 полуоборота(360 градусов) , и разрежьте его посередине. Что получается?
Фокус №3
Изготовьте Лист Мебиуса, который закручен на пол оборота (180 градусов), и начинайте его разрезать отступая все время одну треть от края.
Что получается на этот раз?
Фокус№4
Теперь изготовьте Лист Мебиуса, который закручен на 3 полуоборота (540 градусов), и разрежьте его пополам. У вас должен получиться Лист Мебиуса, который закручен узлом. Вроде этого, но сложнее:

ЮФокус №5
Интересные вещи так же получатся, если сложить бумагу гармошкой, затем скрутить из неё Лист Мёбиуса и резать пополам, или отступая одну треть. Первым делом сделайте гармошку, которая состоит из одного перегиба, образуйте лист Мебиуса поворотом на 360 градусов, и разрежьте посредине. Перед вами предстанут 3 сцепленных между собой кольца.
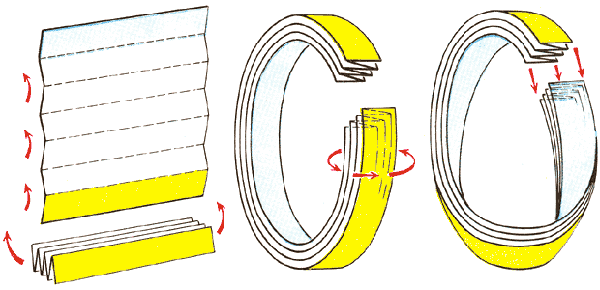
Вы делаете новые и новые Листы, а ведь не каждую полоску можно скрутить в Лист Мебиуса. Например, из квадратного листа бумаги Лист Мебиуса не получится. Тогда какое должно быть минимально отношение длины к ширине полоски, что бы из неё можно было склеить Лист Мебиуса?
Примем для ясности ширину полоски за 1. Оказывается, что минимальная длина полоски равняется v3, это приблизительно 1,73. Полученное значение равно второму «Золотому сечению».
Возникает логичный вопрос: Существуют ли ещё подобные объекты?
Да, существуют, и ещё более замысловатые. Если Лист Мебиуса – «условно двумерный объект» (он получен из плоской полоски), то его подружка - Бутылка Клейна полноправно занимает 3 измерения. Вот как она выглядит:
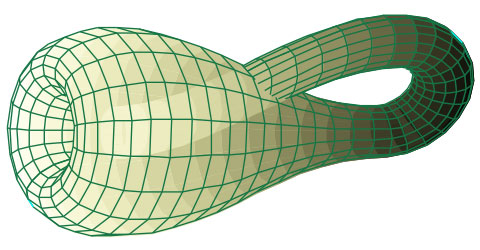
Бутылка Клейна - 3D подружка плоского Мебиуса
Запустите суда муравья, и бедняга побывает во всех точках Бутылки Клейна – не делая в ней дырок, и не переползая через край.
На всех рисунках показано следующее: в месте, где трубка «проникает в бутылку» - нет зазора, хотя это не правильно! Ведь если нет зазора, тогда муравей должен будет выползать из бутылки тем же маршрутом, каким он туда вползал. Разве бродя по Листу Мебиуса ему нужно было разворачиваться после того как он куда то дошёл? Бесконечность, она на то и бесконечность!
А почему мы только обходим Бутылку Клейна? Ведь Лист Мёбиуса мы резали вдоль и поперёк. Что же будет если разрезать Бутылку Клейна?
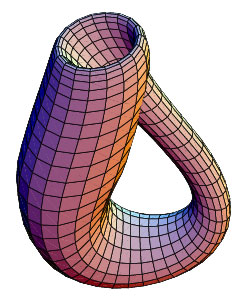
Это невероятно, но получился Лист Мебиуса. Резать, правда, нужно было так, что бы режущий предмет делал оборот в 360 градусов между начальной точкой и конечной.
Бутылка Клейна в трёх измерениях - это аналог Листа Мёбиуса в двух измерениях. Выше вы видели «многослойный» Лист Мебиуса - полученный склеиванием бумаги сложенной «гармошкой». А существуют ли «Многослойные» Бутылки Клейна? Как оказалось – существуют. Назовём их – Бутылки Макса (придумал автор статьи - Максим К.).Вот – обычная Бутылка Клейна:
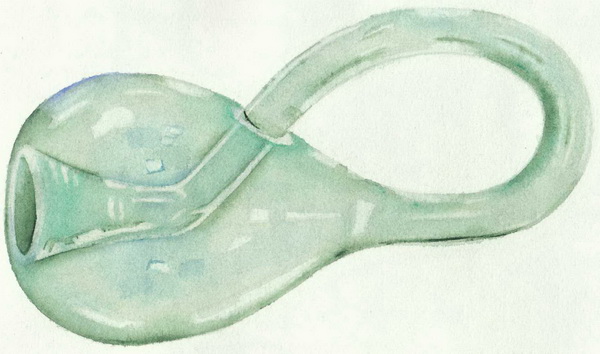
А теперь мысленно представьте себе, как внутри этой бутылки начинает формироваться новая Бутылка Клейна. Сначала внутри образуется «Бутылка Клейна» без «трубки» - бутылка с двумя отверстиями , затем образуется трубка, которая проникает в «трубку» иcходной «Бутылки Клейна», проходит всю «трубку», проникает через отверстие в только что сформировавшуюся «Бутылку Клейна». Затем трубка проникает во второе отверстие основной «Бутылки Клейна ». Находясь в задней части основной бутылки , «трубка» начинает медленно обволакивать исходную «Бутылку Клейна» превращаясь при этом в третью , самую большую «Бутылку Клейна».
Процесс доходит до «трубки» - изначальной «Бутылки Клейна» , и постепенно обволакивает её, затем эта «трубка» проникает только что сформировавшуюся «Бутылку Клейна», затем в исходную, затем в самую маленькую. Проникнув в самую маленькую «Бутылку Клейна », «трубка» доходит до отверстия и сливается с ним.
Получилось что самая маленькая «Бутылка Клейна» перешла в самую большую, и стала с ней одним целым. Ниже рисунок того, что вы пытались вообразить.
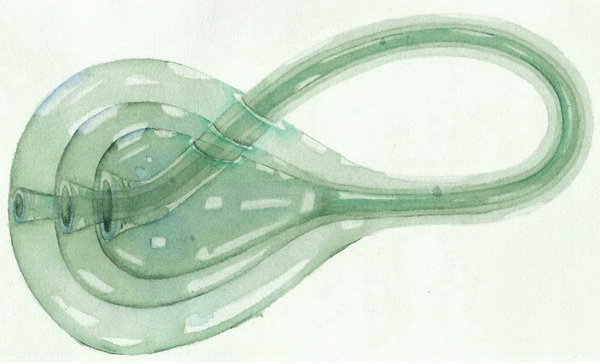
Не обязательно понимать этот мир, нужно лишь найти себя в нем – Альберт Эйнштейн
И всё же, так ли уж нужно ломать голову над тем, как устроен этот мир? Или всё что нам нужно уже есть, и нам остается лишь выбрать «правильный» вариант? Выбор как всегда за вами. Он у вас есть даже в том – делать этот выбор или нет.
По материалам: СОЗЕРЦАЕМ.COM.UA
Dmitry 21.04.2009




41 комментарий
шар (0)
19.12.2013 20:54
сматрите на ютубе как можно вывернуть мяч наизнанку не делая разреза. /там пахлещще мозг раком ставит/
Yury 777 (0)
14.12.2013 21:31
Тема кольца Мебиуса [КМ] уже давным-давно изъезжена вдоль и поперек. Да это и не удивительно. Тысячи людей уже больше 150-ти лет восхищаются КМ и описывают его уникальные свойства. Но, фактически, никаких новых знаний о КМ с увеличением числа публикаций о нем не прибавляется. Все топчутся на одном месте, описывая одни и те же эксперименты с кольцом. rn Однако, интерес к теме не ослабевает. Видимо, загадочная сила этого необычного кольца такова, что оно, как магнит, притягивает и притягивает к себе любознательных. Каждое новое поколение открывает для себя КМ заново. Каждый хочет убедиться во всем на собственном опыте. Поэтому сам клеит, режет и удивляется. rn А недавно было выявлено, что КМ это совсем и не уникум. Что существует целая СИСТЕМА односторонних колец, и кольцо … – только одна из фигур этой системы. rn Если хотите узнать подробнее, зайдите на форум http://moebius.ucoz.com/ . Там есть статья: «Заглянуть за горизонт», в которой приведено описание всей системы односторонних колец. В этой статье, в популярной форме рассказано о том, как можно самому сделать одностороннее кольцо с любым количеством поверхностей, а не только с двумя, как у КМ. И о том, как можно предсказать свойства любого из таких колец, даже не изготавливая его в материале. rn Указанная статья - находка для преподавателей математики и возможность для нынешних школьников и студентов шагнуть дальше своих дедушек и бабушек в познании удивительных свойств односторонних фигур.rn На этом форуме есть ещё много разного интересного материала про кольцо Мебиуса. Причем большая часть материала совершенно уникальная и охватывает не только теоретические, но и возможные практические аспекты применения односторонних колец. Yury-777
aleksandr128 (0)
21.11.2013 18:09
Автор рисунка "тройной бутылки Клейна" вводит читателей в заблуждение. Нельзя построить две и более взаимопараллельные односторонние поверхности. Это нонсенс. Внешняя и внутренняя бутылки суть одна змкнутая "бутылка", естественно, с двумя поверхностями. И только средняя "бутылка" является истинной бутылкой Клейна. http://moebius.ucoz.com .
катя (0)
09.06.2014 08:29
aleksandr128: там ведь написано, что это рисунок того, что вы попытались себе вообразить, ане то, что должно получиться!
Юрий (0)
05.08.2013 19:31
Все, кто интересовался лентой (кольцом) … знают о её удивительном свойстве: она имеет две поверхности, но только одну сторону. Было интересно узнать, можно ли изготовить в материале односторонние кольца, имеющие более двух поверхностей. Мне удалось это сделать и изготовить односторонние кольца, имеющие до 15-ти поверхностей. По аналогии можно изготовить в материале односторонние кольца с любым количеством поверхностей. Эти кольца образуют СИСТЕМУ со своими внутренними объединяющими их закономерностями. Созданы алгоритмы, используя которые можно предсказать показатели колец с любым количеством поверхностей не изготавливая их материальные модели. Как и в случае с кольцом …, материальные модели этих колец может изготовить и повторить любой желающий. Шангин Юрий Александрович E-mail: y.shangin@mail.ru 5 августа 2013г
Георгий (-3)
17.11.2013 19:08
Есть прекрасная статья "Как самому сделать одностороннее кольцо с непредсказуемыми свойствами". Посмотрите форум http://moebius.ucoz.com/ . Там все подробно и понятно расписано. Кстати, материал там не только интересный, но и совсем новый. А то кольцо … уже полтора века все кому не лень обсасывают с разных сторон. А он, как выяснилось, вовсе и не уникум, а всего лишь частный случай односторонних колец. Ну, так у кого хватит пороху попробовать сделать что-то новенькое ?, а не повторять то, что давным - давно изучено со всех сторон.
Андрей (0)
04.02.2013 21:55
я заметил нестыковочку по поводу тройной бутылки клейна)) будь она всего лишь двойной ничего бы не заметил, однако в тройной внутренний пузырь идет самой внутренней трубкой и выходит на внешний большой пузырь, который в свою очередь замыкается на внутренний самый малый пузырь, при этом средний является самостоятельным и не имеющим отношения к двум другим), както так)
Евгения (23)
17.03.2013 15:31
Андрей: Да, вы правы. Получается, что две бутылки обволакивают третью изнутри и снаружи. Хочу попытаться представить большее количество бутылок.
Сергей (42)
28.10.2012 13:24
Очень интересная статья. И с юмором, что немаловажно)
Оля (3)
18.03.2012 07:27
Жаль что задачка с домиками не решается:(
альфа (0)
29.02.2012 19:30
как можно сложить ленту гормошкой и получить 3 кольца
Сергей (42)
20.04.2011 13:28
1974 год, Белорусский Политех, энергофак, 1-й курс, матанализ. С удовольствием вспомнил.
фрау Марта (5)
23.01.2011 00:46
бутылка Клейна - идеальный манеж для младенца-ползуна: запускаешь в узкое горлышко, а как доползет до условного дна-переворачиваешь узким кверху! Хотя обратно вытряхивать тяжелоооо будет…
Meelman (0)
24.09.2010 15:04
можно обойти без дырки только в 4 измерении
Алик (0)
29.07.2010 00:24
Очень забавные парадоксы! понравились)) Очень умно!
Ёлы Палыч (3)
28.09.2012 16:15
Алик: Тут нет парадоксов, только видимость. Топология - она такая
Мосинька (-150)
22.01.2010 01:30
уоу!! у меня вытек моск)) на бутылке). "Созерцаем" (сайт) - не то слово, лучше было назвать "Втыкаем"… Но вообще, забавная выходит ситуация: время полвторого ночи, вставать рано, муж уже в постели, злится, а я… вырезаю из блокнотика полоски и со степлером и ножницами "ленты Мебиуса" кручу) Вещь!
муль (52)
15.12.2009 08:36
Над задачкой покряхтел. Пытался сделать разные варианты. А потом прочитал что она не решается.
Dragon Tear (1)
20.11.2009 15:32
Сижу в ворохе бумаги, коллеги смотрят как на психа.. Классная статья!! ^_^
Notimer (0)
04.09.2009 13:20
Вообще, Barraf прав о циркуляции воды в попытках наполнить бутылку =) Тут - как с лентой Мебиуса: муравей успеет побывать на обоих краях, не переползая, так же как и вода будет наполнять как "внутреннюю" так и "наружную" поверхности бутылки - то бишь одну и ту же. Но в эвклидовом пространстве без пересечения собственной поверхности нельзя - зато это прекрасно действует в 4х-мерном пространстве. А получить бутылку можно путем склеивания ленты Мебиуса по краям))
Осьминог (8)
19.07.2009 00:11
С Мебиусом всё ясно. А вот по поводу бутылки… Так и не поняла, как возможно её обойти изнутри и снаружи, не пересекая границ горлышка… Вообще сейчас мозг сломаю.
Плоский философ (4)
14.06.2009 16:06
Без зазора бутылку точно не перелезть, как ленту Мебиуса. А с зазором как-то неубедительно ощущается бесконечность.
Борис (-13)
10.06.2009 23:41
покури и втыкай
XAVEN (-12)
01.05.2009 15:56
Блин, а год назад я пытался решить эту задачку с водой огнем и электричеством и у меня никак не выходила - окола часа на просрал)а так очень интересно)
1 (-28)
01.05.2009 11:22
круто
SeAlUs (0)
30.04.2009 11:42
А вот многослойную бутылку Клейна автор визуализировал не совсем хорошо: на рисунке только малая и большая бутылки переходят друг в друга, а средняя как бы вписана в пространство между ними
SeAlUs (0)
30.04.2009 11:36
Само физическое представление бутылки, конечно, не идеально, и про возможность её наполнения говорить сложно, но в описанном случае (когда жидкость проникает в сосуд по стенкам) она не наполняема. Шар же со сквозной дырой не удовлетворяет условиям одноповерхностного объекта, так как нельзя обойти всю его поверхность, не перелезнув через край, коих у него два.
Аллекс (0)
28.04.2009 23:33
Эти забавные задачки по топологии я еще в детстве узнала - книжка попалась. Еще что-то про раскрашивание карт было, тоже увлекательно, пробуждает воображение
ленка (1)
27.04.2009 12:28
или я чего-то не понимаю, или эту бутылку также легко можно наполнить водой, как и обычную. только горлышко внизу. И таковой бутылкой сожет являться обычный шар со сквозной дырой не так ли??
Koobraa (94)
23.04.2009 20:29
Вообще классная тема - изрезала кучу бумаги. С детства так не радовалась!
Koobraa (94)
23.04.2009 20:28
Asahitarou молодец - электричество идёт по воде :)
Денис (9)
23.04.2009 10:17
Piglette, речь идёт о том, чтобы "испозать" всю бутылку, не перелезая через край. А краем, разделяющим две поверхности, является каёмка горлышка (так же как на закрученном листке краем является его ребро и через него не нужно перелазить, чтобы обойти весь лист). Хотя, аналогию и я нахожу сомнительной, потому что, как ты сказала "как это бесконечная поверхность, если в ней зазор?". Возможно пробема в том, что в случае с листком мы двухмерную фигуру превращаем в трёхмерную.
Денис (9)
23.04.2009 10:16
Piglette, речь идёт о том, чтобы "испозать" всю бутылку, не перелезая через край. А крайем, разделяющим две поверхности является каёмка горлышка (точно так же как на закрученном листке краем является его ребро и через него не нужно перелазить, чтобы обойти весь лист). Хотя, аналогию и я нахожу сомнительной, потому что, как ты сказала "как это бесконечная поверхность, если в ней зазор?".Возможно пробема в том, что в случае с листком мы двухмерную фигуру превращаем в трёхмерную.
HEKTO (-1)
22.04.2009 21:56
Asahitarou, так делать нельзя, т.к. все три тропинки выходят из одной точки и прходят в другие три, таким образом, делая так, вы пересекаете линию.
Лекс (20)
22.04.2009 03:44
Короткий фантастический рассказ на эту тему Нульсторонний профессор, любопытным советую почитать
Piglette (136)
21.04.2009 23:46
спасибо, Barraf! только я все равно не понимаю: как это бесконечная поверхность, если в ней зазор? какая тут аналогия с лентой мебиуса?
Li14 (1)
21.04.2009 20:42
С задачей с домиками всё решается при использовании правой кнопки мыши.
Barraf (0)
21.04.2009 19:19
Чтобы разорбаться ещё лучше, представь что в бутылку Клейна заходит жидкость и начинает течь вперёд (вглубь) одновремнно по всей внутренней поверхности. Жидкость выходит наружу и потом опять попадает внутрь не прекращая ход (не забывай про зазор на входе горлышка в саму бутылку). В обычной бутылки если вода начинает стекать по стенкам она попадает на дно и замыкается начиная наполнять сосуд.
Barraf (0)
21.04.2009 19:17
to Piglette. Могу ошибаться, но горлышко у бутылки, это как край у полоски. Представь бумажную бутылку, у неё горлышко - однозначный край объекта. У бутылки Клейна края нет. Горлышко и дно - это одно и то же. Внутрянняя и внешняя поверхности - это одна и та же поверхность.
Piglette (136)
21.04.2009 17:24
изрезала два листа а4:) очень интересно. я вот только чего не понимаю. разве не любая бутылка является бесконечной поверхностью (ну или как там она правильно называется…)? ведь можно исползать все внутри бутылки, потом переползти через горлышко и поползать по внешней стороне. конечно, я не права, иначе физики не стали бы ничего выдумывать:) но кто бы объяснил, почему я не права…
Фенечка (0)
21.04.2009 16:43
Класс!!