Магический квадрат (волшебный квадрат)

Квадрат 3x3
Магический, или волшебный квадрат — это квадратная таблица n×n, заполненная n2 числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n2. Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n2 + 1.
Квадрат Ло Шу - единственный нормальный магический квадрат 3×3. Был известен еще в Древнем Китае, первое изображение на черепаховом панцире датируется 2200 до н.э.
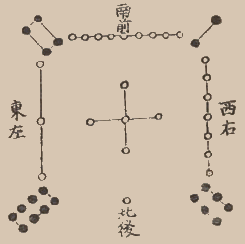
Изображение Ло Шу в книге эпохи Мин
| 4 | 9 | 2 | |
| 3 | 5 | 7 | |
| 8 | 1 | 6 |
| 7 | 12 | 1 | 14 |
| 2 | 13 | 8 | 11 |
| 16 | 3 | 10 | 5 |
| 9 | 6 | 15 | 4 |
Дьявольский магический квадрат — магический квадрат, в котором также с магической константой совпадают суммы чисел по ломаным диагоналям (диагонали, которые образуются при сворачивании квадрата в тор) в обоих направлениях. Такие квадраты называются ещё пандиагональными. Существует 48 дьявольских магических квадратов 4×4 с точностью до поворотов и отражений.
Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве. Два средних числа в нижнем ряду указывают дату создания картины (1514).

Магический квадрат 4×4, изображённый на гравюре Альбрехта Дюрера «Меланхолия I», считается самым ранним в европейском искусстве.
Сумма чисел на любой горизонтали, вертикали и диагонали равна 34. Эта сумма также встречается во всех угловых квадратах 2×2, в центральном квадрате (10+11+6+7), в квадрате из угловых клеток (16+13+4+1), в квадратах, построенных «ходом коня» (2+8+9+15 и 3+5+12+14), в прямоугольниках, образованных парами средних клеток на противоположных сторонах (3+2+15+14 и 5+8+9+12). Большинство дополнительных симметрий связано с тем, что сумма любых двух центрально симметрично расположенных чисел равна 17.
Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата: нечетен, равен удвоенному нечетному числу или равен учетверенному нечетному числу. Общий метод построения всех квадратов неизвестен, хотя широко применяются различные схемы.
Шахматный подход. Известно, что шахматы, как и магические квадраты, появились десятки веков назад в Индии. Поэтому неслучайно возникла идея шахматного подхода к построению магических квадратов. Впервые эту мысль высказал Эйлер. Он попытался получить полный магический квадрат непрерывным обходом коня. Однако, это сделать ему не удалось, поскольку в главных диагоналях суммы чисел отличались от магической константы. Тем не менее шахматная разбивка позволяет создавать любой магический квадрат. Цифры заполняются регулярно и построчно с учетом цвета ячеек.

Изображение схем построения магических квадратов.
Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7-ми планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.
Судоку - магический квадрат
Любителям магических квадратов предлагаем развеяться и поиграть в судоку. Судоку — это головоломка-пазл с числами, ставшая в последнее время очень популярной. В переводе с японского "су" — "цифра", "доку" — "стоящая отдельно". Иногда судоку называют «магическим квадратом». Игровое поле представляет собой квадрат размером 9x9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В некоторых из них уже в начале игры стоят числа (от 1 до 9). В зависимости от того, сколько клеток уже заполнены, конкретную судоку можно отнести к лёгким или сложным.
Dmitry 03.03.2009
Почему чиновники и почта плохо работают?
Попробуйте угадать название всех недетских фильмов по детским рисункам
Предки человека и обезьян пришли в Африку из Азии
Как нарисовать человека
Ученые доказали связь депрессии и самобичевания
73 комментария
Света (-23)
07.12.2015 15:41
крутооо!
ваше имя (-3)
18.02.2015 19:15
это бред
Софья (0)
02.02.2015 19:25
я теперь умею решать магический квадрат!УРА!
Марина (33)
30.03.2015 13:28
Софья: ты полна при полна умница
лера (0)
22.01.2015 11:43
1 ая строка,3ая клетка цифра62.2ая строка,1ая клетка54,2ая клетка18.3ая строка,1ая клетка14.
Анна (-90)
27.11.2014 13:48
что значит нормально? эльза ты дура или чё ты наверное тупая ах да тебе наверно 6 лет дура ты не грамотная
Пацан (0)
27.11.2014 14:05
Анна: …
Пацан (0)
27.11.2014 13:51
Анна: слыш ты анна или как там тебя ты мою сестру не обзывай а то найду как врежу мало не покажится …!
Эльза (0)
27.11.2014 13:18
хммм….нормально!
Елена (56)
24.11.2014 21:14
Нужно составить магический квадрат 4 на 4 с числами 2 4 6 8.
Софья (0)
20.10.2014 18:41
Помогите решить 7?3 ?6? 9??
Софья (0)
20.10.2014 18:40
Помогите решить 7?3 ?6? 9??
Индира (5)
20.10.2014 11:37
Как получить магически квадрат заполнив любыми цифрами получить 13. 13 это сумма чисел одной строки или столбца
катя (0)
10.09.2014 19:40
Помогите.
Анна (-90)
26.08.2014 00:44
? ? 29 ? 25 ? 31 ? 30
Макс (7)
21.03.2014 17:25
помогите в первом столбике 9 4 5 во втором нету а в третем во 2 линии 8
Леонид (-57)
15.03.2014 08:58
помогите мне пажалуста ыыы 18?16 ?15? 17??
lbvf (0)
06.03.2015 01:36
Леонид:
Роман (-17)
23.02.2015 18:15
Леонид:
Ольга (-8)
13.03.2014 09:34
Квадрат 3 на 3. Первый ряд- пустой. Второй ряд- первая клетка пустая, вторая число15, третья 9. Третий ряд - первая и вторая клетки пустые, третья клетка 24. Большое спасибо!
галина (2)
18.03.2014 00:47
Ольга: Первая строка: 6 27 12 Вторая 21 15 9 Третья 18 3 24
Ольга (-8)
13.03.2014 09:29
Помогите пожалуйста решить магический квадрат, 3й класс. / / / /15/9 / / /24/
Юрий (12)
06.03.2014 00:28
Здравствуйте! А не подскажите как пользоватьса магическим квдратом волшебном так называемый 15.С уважением.Юрий.
Настя (-399)
21.02.2014 17:52
Можете помочь срочно!Нужно заполнить квадрат 4 на 4 так чтобы в любой строке сумма чисел была равна 0, а в любом столбце отрицательному числу, плиз.ПОМОГИТЕ СРОЧНО!
мария сушкина твер (0)
04.02.2014 15:25
классс
Илья (0)
08.07.2013 06:10
http://vk.com/club55628960 Это группа В Контакте по судоку (оригинальные судоку).
лёля котова (0)
15.05.2013 19:08
привет я учусь играть в судоку
Viktor (2)
14.03.2013 14:46
как решить магический квадрат там можно брать только числа 1 2 3
Nastyusha (0)
03.04.2014 18:15
помогите решить магический квадрат чтобы сумма числа была 15, но чтобы числа не повторялись
Юля (0)
19.04.2013 01:53
Viktor:
sofia (0)
21.02.2013 09:57
Дано 80 90 0 50 помоги а!!
Костя (0)
30.01.2013 23:09
дано 4.5.6.7.8.9.10.11.12 составь магический квадрат 3/3
Ал (-24)
17.12.2012 22:25
Можите решить с числами 111, 118, 113, и. т. г.ааа?
Лутчший (0)
17.12.2012 22:09
Вроде такие взрослые а ведёте себя как маленькие!
Zaka (0)
22.11.2012 15:46
Решите задачу Эйнштейна.Он интересный
Logvienco (0)
22.11.2012 23:34
Zaka: решил за 5 минут)
Мария (-2)
04.02.2014 15:24
пипец
Ната (4)
15.10.2011 18:33
Блина я не могу сделать ну неполучается … что делать?
Света (-23)
29.05.2012 12:25
Ната: Даны числа: 2, 3, 4, 5, 6, 7, 8, 9, 10. Требуется вписать их в клетки квадрата так, чтобы в любом направлении в сумме получилось одно и то же число. Часть чисел уже вписана в квадрат
Света (-23)
29.05.2012 12:23
Ната: . Даны числа 1, 2, 3, 4, 5, 6, 7, 8, 9. Часть из них расставлена по клеткам Требуется расставить остальные числа, чтобы в сумме получалось 15. попробуй!
ХуЛиГаНкА (0)
15.10.2011 14:50
У меня не получилось…
Miss Kawaii (0)
20.09.2011 17:41
Блин, оказалось так легко! Нам в 5 классе дофига таких задас задают ….
215412574218з (0)
05.07.2011 16:50
Круто.
кын (0)
23.05.2011 14:55
блин где можно их записать?
Женя (-19)
27.04.2011 08:15
Да ето легкотня!!нужно заполнять пустые клетки так что-бы числа в каждом столбике или строчке неповторялись…)Всё просто.
Gintoki (86)
16.01.2011 08:25
Вроде так просто, но боюсь, что мне этого не понять и ни одно судоку не решить:)
юляша (1)
13.12.2010 09:55
БЛИН… НЕ МОГУ ПОНЯТЬ!
Юля (1)
13.12.2010 09:53
а можно по подробней???
Сашка (29)
05.03.2011 12:52
Юля: юляша: ты есть в контакте
Сашка (29)
05.03.2011 12:50
Юля:
Настя (0)
05.11.2010 10:56
Круто! У меня не получалось.До сих пор не пойму как они это делают.
Маргулан (0)
14.10.2010 12:21
Trados: не знаю.Скажи!
Trados (-599)
19.07.2010 10:41
Да! Я знаю такой квадрат, играл в один квест, так вот там какойквадрат нужно было составить, в каждом столбике и строчке сумма чисел равна 55
Бекс (0)
28.02.2010 21:27
как можно найти 7х7 Магический квадрат
Мосинька (-150)
22.01.2010 01:58
Квадраты попроще тоже решала в школе. А вот квадрат 4*4, в котором чуть ли не любые 4 числа равны одной и той же сумме, впечатлил. Даже после объяснения, которое показало, что, в целом, мы можем если не придумать, то хоть воспроизвести такой квадрат, всё равно впечатление!) 3*3 гораздо проще, потому что там в разы меньше осей, по которым должна получаться нужная сумма
сергей 074 (0)
07.10.2009 18:09
уважаемые ,а как насчет игры 15 . сложите магический квадрат из этих фишек . причем обе диагонали равны горизонтали и вертикали.решение реально существует.
апн (0)
14.10.2010 12:22
сергей 074:
барабула (0)
15.09.2009 18:03
сложно
рпрп (-1)
15.09.2009 17:51
фууу
ber_viking (0)
08.09.2009 22:30
to курбельrn> 3х3 и из чисел 1,2,3rnrnТак это вас просили латинский квадрат нарисовать.rnrnЧто касается квадратов других порядков, раньше это могли лучшие математики, сегодня это входит в школьный курс. Закончили школу и "шарики" закцикливают от "квадратов" - идите в менагеры.
oksano4ka (-1)
05.08.2009 03:18
Откройте учебник по математике за 1 класс Л.Петерсон, там и не такие квадраты магические увидите! Ничего сложного в них нет.
SchneeWittchen (1)
24.04.2009 17:07
А я помню в третьем классе такие задачи 3на 3! И я их щелкала!
453454 (0)
20.04.2009 20:25
Посетители твоего сайта смогут размщать рекламу исключительно у тебя при помощи iQela.ru
Иваська (-1)
14.03.2009 18:44
Нет, ну какможносделатьквадрат 3 на 3 я понимаю: * 5 в центре потому, что она не имеет пары. * 9, 8, 7 не дожнынаходиться на одной прямой потому,что в суме любые два из них дают нужный результат, если не больше… Дальше интуитивно доставитьцифры, это уже не сложно. С 4 на 4 тоже более-менее понятно. Представленные 2 квадрато очень похожи. C той лишь разницей, что числа в первом стоят в рядах, а во втором квадратами. Других симетрий я не вижу. Но 5,6,7,8,9 - это НЕРЕАЛЬНО!
курбель (13)
10.03.2009 09:31
Как можно сделать?Ха-ха!Я тоже не понимаю,а дочери (3 класс) на дом задают!3х3 и из чисел 1,2,3-попробуйте!У меня одна диагональ получается из какой либо одной цифры…После нескольких безуспешных попыток,сообщил дочке,что тройки,в школе,мне ставили из ЖАЛОСТИ=)ПОТОМУ ЧТО Я ТУПОЙ=)
XAVEN (-12)
03.03.2009 22:23
Как так можно сделать!ваще)