Интеллектуальные развлечения. Интересные иллюзии, логические игры и загадки.

Принципы построения иллюзий

Иллюзорные произведения искусства имеют определенное обаяние. Они - триумф изобразительного искусства над действительностью. Почему иллюзии так интересны? Почему так много художников используют их в своих произведениях? Возможно, потому что они показывают не то, что нарисовано на самом деле. Все отмечают литографию "Водопад" ("Waterfall") Мориса Эшера (Maurits C. Escher). Вода здесь циркулирует бесконечно, после вращения колеса она течет дальше и попадает обратно в исходную точку. Если бы такую конструкцию можно было бы построить, то был бы вечный двигатель! Но при более внимательном рассмотрении картины мы видим, что художник обманывает нас, и любая попытка построить эту конструкцию обречена на неудачу.

Изометрические рисунки

Для передачи иллюзии трехмерной действительности используются двухмерные рисунки (рисунки на плоской поверхности). Обычно обман состоит в изображении проекций твердых фигур, которые человек пытается представить как трехмерные объекты в соответствии со своим личным опытом.

Классическая перспектива эффективна при имитировании действительности в виде "фотографического" изображения. Это представление неполно по нескольким причинам. Оно не позволяет нам видеть сцену с различных точек зрения, приблизиться к нему или рассмотреть объект со всех сторон. Оно не дает нам и эффекта глубины, которую реальный объект имел бы. Эффект глубины возникает из-за того, что наши глаза смотрят на объект с двух разных точек зрения, и наш мозг их совмещает в одно изображение. Плоский рисунок представляет сцену только с одной определенной точки зрения. Примером такого рисунка может быть фотография, сделанная при помощи обычного монокулярного фотоаппарта.

При использовании этого класса иллюзий, рисунок кажется на первый взгляд обычным представлением твердого тела в перспективе. Но при более близком рассмотрении становятся видны внутренние противоречия такого объекта. И становится ясно, что такой объект не может существовать в действительности.

Иллюзия Пенроуза

Водопад Эшера основан на иллюзии Пенроуза, называемой иногда иллюзией невозможного треугольника. Здесь эта иллюзия проиллюстрирована в своей простейшей форме.

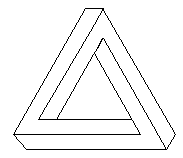
Кажется, что мы видим три бруска квадратного сечения соединенных в треугольник. Если Вы закроете любой угол этой фигуры, то увидите, что все три бруска соединены правильно. Но когда Вы уберете руку с закрытого угла, то станет очевиден обман. Те два бруска, которые соединятся в этом угле, не должны быть даже вблизи друг друга.

В иллюзии Пенроуза используется "ложная перспектива". "Ложная переспектива" используется также и при построении изометрических изображений. Иногда такая перспектива называется китайской (прим. переводчика: Реутерсвард называл такую перспективу японской). Такой способ рисования часто использовался в китайском изобразительном искусстве. При таком способе рисования глубина рисунка двусмысленна.

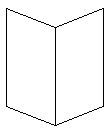В изометрических рисунках все параллельные линии представляются параллельными, даже если они наклонены по отношению к наблюдателы. Объект, имеющий угол наклона, направленный от наблюдателя, выглядит точно так же , как если бы он был наклонен к наблюдателю на тот же угол. Прямоугольник согнутый вдвое (фигура Мача (Mach)) ярко показывает такую двусмысленность. Эта фигура может показаться вам раскрытой книгой, как будто вы смотрите на страницы книги, или может показаться книгой, развернутой к вам переплетом и вы смотрите на обложку книги. Эта фигура также может казаться двумя совмещенными параллелограммами, но очень небольшое количество людей увидят эту фигуру именно в виде параллелограммов.

Фигура Тьери (Thiery) иллюстрирует ту же двойственность

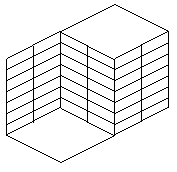
Рассмотрим иллюзию лестницы Шроедера (Schroeder) - "чистый" пример изометрической двусмысленности глубины. Эта фигура может быть воспринята как лестница, по которой можно было подниматься справа налево, или как вид лестницы снизу. Любая попытка изменить положение линий фигуры разрушит иллюзию.

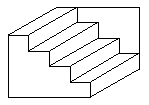
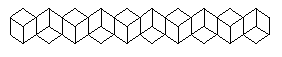
Этот простой рисунок напоминает линию кубиков, показанных то снаружи то изнутри. С другой стороны этот рисунок напоминает линию кубиков, показанных то сверху, то снизу. Но очень трудно воспринять этот рисунок как просто набор параллелограммов.

Закрасим некоторые области черным. Черные параллелограммы могут выглядеть так, как будто мы на них смотрим или снизу или сверху. Попробуйте, если сможете, увидеть эту картину по-другому, как будто на один параллелограмм мы смотрим снизу, а на другой сверху, чередуя их. Большинство людей не может воспринять таким образом эту картину. Почему мы не способны воспринять картину таким образом? Я считаю, что это наиболее сложная из простых иллюзий.

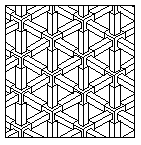На рисунке справа используется иллюзия невозможного треугольника в изометрическом стиле. Это - один из образцов "штриховки" программы для черчения AutoCAD (TM). Данный образец называется "Escher".

Изометрический рисунок проволочной конструкции куба показывает изометрическую двусмысленность. Эта фигура иногда называется кубом Некера (Necker cube). Если черная точка находится в центре одной сторон куба, то является ли эта сторона лицевой стороной или задней? Вы также можете представить, что точка находится около правого нижнего угла стороны, но вы все равно не сможете сказать, является ли эта сторона лицевой или нет. У вас также не может быть причин предполагать, что точка находится на поверхности куба или внутри него, она с тем же успехом может быть и перед кубом и за ним, так как мы не имеем никакой информации о реальных размерах точки.

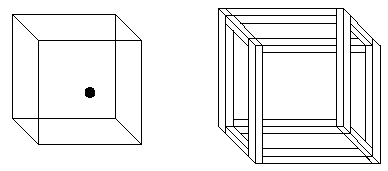Если представить себе грани куба в виде деревянных планок, то можно получить неожиданные результаты. Здесь мы использовали неоднозначное соединение горизонтальных планок, о котором будет рассказываться ниже. Эта версия фигуры называется невозможным ящиком. Она является основой для многих аналогичных иллюзий.

Невозможный ящик не может быть сделан из древесины. И все же мы видим здесь фотографию невозможного ящика сделанного из дерева. Это - обман. Одна из планок ящика, которая, как кажется, проходит позади другой, на самом деле является двумя отдельными планками с разрывом, одна ближе, а другая дальше чем пересекающая планка. Такая фигура видна только с единственной точки зрения. Если бы мы смотрели на реальную конструкцию, то при помощи нашего стереоскопического зрения мы бы увидели уловку, за счет которой фигура становится невозможной. Если бы мы сменили точку зрения, то эта уловка стала бы еще заметнее. Именно поэтому при демонстрации невозможных фигур на выставках и в музеях вы вынуждены смотреть на них сквозь маленькое отверстие одним глазом.

Невозможный ящик не может быть сделан из древесины. И все же мы видим здесь фотографию невозможного ящика сделанного из дерева. Это - обман. Одна из планок ящика, которая, как кажется, проходит позади другой, на самом деле является двумя отдельными планками с разрывом, одна ближе, а другая дальше чем пересекающая планка. Такая фигура видна только с единственной точки зрения. Если бы мы смотрели на реальную конструкцию, то при помощи нашего стереоскопического зрения мы бы увидели уловку, за счет которой фигура становится невозможной. Если бы мы сменили точку зрения, то эта уловка стала бы еще заметнее. Именно поэтому при демонстрации невозможных фигур на выставках и в музеях вы вынуждены смотреть на них сквозь маленькое отверстие одним глазом.

Неоднозначные соединения

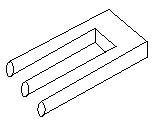
На чем основывается эта иллюзия? Является ли она разновидностью книги Мача?

Фактически, это - комбинация иллюзии Мача и неоднозначного соединения линий. Две книги разделяют общую среднюю поверхность фигуры. Это делает наклон книжной обложки неоднозначной.

Иллюзии положения

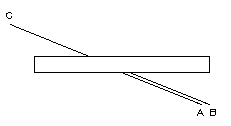Иллюзия Поггендорфа (Poggendorf), или "пересеченный прямоугольник", вводит нас в заблуждение, какая из линий A или B является продолжением линии C. Однозначный ответ можно дать только, приложив линейку к линии C, и проследив, какая из линий с ней совпадает.

Иллюзии формы

Иллюзии формы тесно связаны с иллюзиями положения, но здесь сама структура рисунка заставляет изменять наше суждение о геометрической форме рисунка. На приведенном ниже примере короткие наклонные линии создают иллюзию, что две горизонтальные линии изогнуты. На самом деле - это прямые параллельные линии.

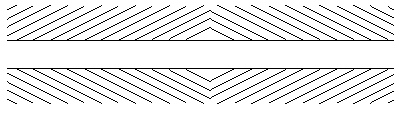
В этих иллюзиях используется особенность нашего мозга обрабатывать видимую информацию, в том числе штрихованные поверхности. Один образец штриховки может доминировать настолько сильно, что другие элементы рисунка кажутся искаженными.

Классический пример - набор концентрических кругов с наложенным на них квадратом. Хотя стороны квадрата абсолютно прямые, они кажутся изогнутыми. То, что стороны квадрата прямые можно убедиться, приложив к ним линейку. На этом эффекте основаны большинство иллюзий формы.

На том же принципе работает следующий пример. Хотя оба круга имеют один и тот же размер, один из них выглядит меньше другого. Это - одна из многих иллюзий размера.

Объяснением подобному эффекту может служить наше восприятие перспективы на фотографиях и картинах. В реальном мире мы видим, что две параллельные линии сходятся при увеличении расстояния, поэтому мы воспринимаем, что круг, касающийся линий, находится дальше от нас и, следовательно, должен быть большего размера.

Если круги закрасить черным цветом круги и области, ограничиваемые линиями, то иллюзия будет слабее.

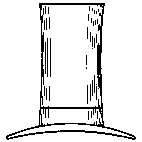
Ширина полей и высота шляпы одинаковы, хотя так и не кажется на первый взгляд. Пробуйте повернуть изображение на 90 градусов. Сохранился ли эффект? Это - иллюзия относительных размеров в пределах картины.

Неоднозначные эллипсы

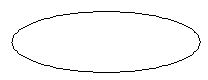
Наклоненные круги проецируются на плоскость эллипсами, и эти эллипсы имеют двусмысленность глубины. Если фигура (выше) представляет собой наклоненный круг, то не нет способа узнать, находится ли верхняя дуга ближе к нам или дальше от нас, чем нижняя дуга.

Неоднозначное соединение линий является существенным элементом в иллюзии неоднозначного кольца:

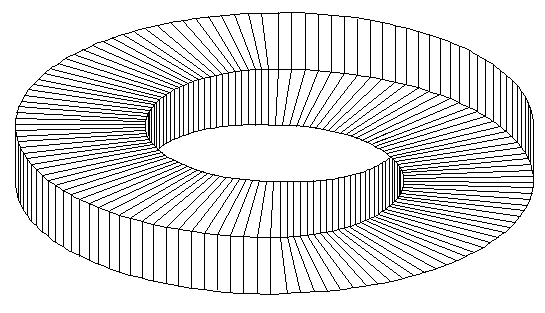
Неоднозначное кольцо, © Дональд Е. Симанек, 1996.

Если закрыть половину картины, то остальная часть будет напоминать половину обычного кольца.

Когда я придумал эту фигуру, я думал, что это она могла бы стать оригинальной иллюзией. Но позже я увидел рекламу с эмблемой корпорации, выпускающей оптоволокно, Canstar. Хотя эмблема Canstar моей, их можно отнести к одному классу иллюзий. Таким образом, я и корпорация разработали независимо друг от друга фигуру невозможного колеса. Думаю, если капнуть глубже, то, вероятно, можно найти и более ранние примеры невозможного колеса.

Бесконечная лестница

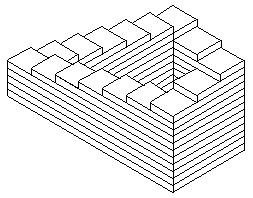Еще одна из классических иллюзий Пенроуза - невозможная лестница. Она чаще всего изображается в виде изометрического рисунка (даже в работе Пенроуза). Наша версия бесконечной лестницы идентична версии лестницы Пенроуза (за исключением штриховки).

Она также может быть изображена и в перспективе, как это сделано на литографии М. К. Эшера.

Обман на литографии "Восхождение и спуск" строится несколько иным способом. Эшер поместил лестницу на крышу здания и изобразил здание ниже таким образом, чтобы передать впечатление перспективы.

Художник изобразил бесконечную лестницу с тенью. Как и штриховка, тень могла бы уничтожить иллюзию. Но художник поместил источник света в таком месте, что тень хорошо сочетается с другими частями картины. Возможно, тень от лестницы является иллюзией сама по себе.

Заключение

Некоторых людей нисколько не интригуют иллюзорные картины. "Всего лишь неправильная картина" - говорят они. Некоторые люди, возможно меньше 1% населения, не воспринимают их, потому что их мозг не способен преобразовывать плоские картины в трехмерные образы. Эти люди, как правило, испытывают сложности в восприятии технических чертежей и иллюстраций трехмерных фигур в книгах.

Другие могут увидеть, что с картиной "что-то неправильно", но они и не подумают спросить, каким образом получается обман. У этих людей никогда не возникает потребности понять, как работает природа, они не могут сосредоточиться на деталях за недостатком элементарного интеллектуального любопытства.

Возможно, понимание визуальных парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Среди работ М. К. Эшера (M.C. Escher) есть очень много картин-иллюзий, а также сложных геометрических картин, которые можно отнести скорее к "интеллектуальным математическим играм", чем к искусству. Однако, они производят впечатление на математиков и ученых.

Говорят, что люди, живущие на каком-нибудь тихоокеанском острове или глубоко в джунглях Амазонки, где никогда не видели фотографии, не смогут сначала понять, что изображает фотография, когда им ее покажут. Интерпретация этого специфического вида изображения является приобретенным навыком. Одни люди овладевают этим навыком лучше, другие - хуже.

Художники начали использовать геометрическую перспективу в своих работах значительно раньше изобретения фотографии. Но они не могли изучить ее без помощи от науки. Линзы стали общедоступными только в XIV столетии. В то время они использовались в экспериментах с затемненными камерами. Большая линза помещалась в отверстие в стенке затемненной камеры так, чтобы перевернутое изображение отображалось на противоположной стенке. Добавление зеркала позволяло отбрасывать изображение пол потолок камеры. Это устройство часто использовалось художниками, которые экспериментировали с новым "европейским" перспективным стилем в художественном искусстве. К тому времени математика уже была достаточно сложной наукой, чтобы дать теоретическое обоснование перспективы, и эти теоретические принципы были опубликованы в книгах для художников.

Только самостоятельно пробуя рисовать иллюзорные картины можно оценить все тонкости необходимые для создания подобных обманов. Очень часто природа иллюзии накладывает свои ограничения, навязывая свою "логику" художнику. В итоге, создание картины становится сражением остроумия художника со странностями нелогичной иллюзии.

Теперь, когда мы обсудили суть некоторых иллюзий, вы можете использовать их, чтобы создавать собственные иллюзии, а также классифицировать любые иллюзии, которые вам встретятся. Через некоторое время вы будете иметь большую коллекцию иллюзий, и вам необходимо будет каким-то образом демонтрировать их. Я разработал для этого стеклянную витрину.

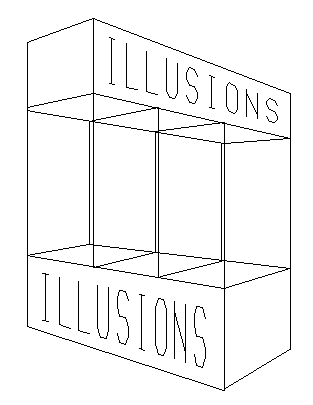
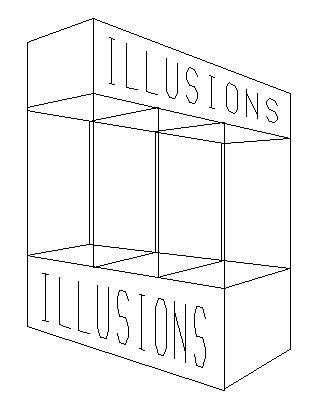
Витрина иллюзий. © Дональд Е. Симанек, 1996.

Вы можете проверить сходимость линий в перспективе и другие аспекты геометрии этого рисунка. Анализируя такие картины, и пробуя рисовать их, можно узнать суть обманов, используемых в картине. М. К. Эшер (М. C. Escher) использовал подобные уловки в своей картине "Бельведер" (ниже).

Дональд Е. Симанек, декабрь 1996. Перевод с английского Влада Алексеева.

Dmitry   04.05.2005