Задачка про домино
Задачка для школьников, даже не совсем задачка, а скорее повод к размышлению. Задумайтесь.
Если положить одну костяшку домино на другую, то, чтобы не упала верхняя, ее нужно положить на расстояние чуть менее L/2, где L - длина костяшки домино. На какое расстояние нужно положить третью костяшку? Четвертую? Сколько вообще костяшек можно поставить одну на другую, чтобы они не упали?
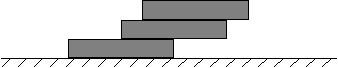
Можно ли собрать такую пирамидку, чтобы проекция на плоскость самой верхней костяшки лежала вне основания самой нижней?
Dmitry 26.03.2009




38 комментариев
Оля (3)
18.03.2012 08:17
Это невозможно! Если конечно не применять клей:)
mr.GISH(он же Clark) (537)
13.06.2011 20:01
да тут просто первую костяшку нужно прибить гвоздём к полу, а остальные костяшки приклеивать друг к другу супер клеем и ничё сложного)
Yegor (4)
26.04.2011 17:27
Нельзя. Читай Ахилес и черепаха.
Комментарий Tarik скрыт. Посмотреть, что он написал.
Tarik (-13)
21.02.2011 22:34
Ответ бесконечное количество доминошек. Это как задача про Ахиллеса и Черепаху.
Футаме (0)
09.02.2011 20:32
Если мы сразу положим вторую костяшку на L/2, то для того, чтобы она не упала надо чтобы все остальные (3,4..) лежали строго на второй. Иначе центр тяжести системы из n костяшек выйдет за пределы первой костяшки.
toll (-5)
04.02.2011 12:41
Как только центр тяжести верхних 2-х или более домино выйдет за пределы опоры (самой нижней домино) - они упадут. Поэтому ответ на Ваш вопрос отрицательный.
Комментарий Игоиь скрыт. Посмотреть, что он написал.
Игоиь (-9)
07.01.2011 23:47
да можно
Волна китайских панд (31)
13.12.2010 14:43
Для меня это слишком сложно. Три точно можно положить, чтоб держалось. Свыше - будет падать. Мне так кажется. Под рукой
михаил 39л (0)
16.10.2010 17:53
вообще то можно и на 1 костяшку стоящую ребром поставить все 27 доминушек
Евгений (0)
23.11.2010 20:54
михаил 39л:
Evgeny marsianin (-1)
17.07.2010 13:09
можно так положить 139 доминошек.., больше у меня не оказалось(((
AlexBoboshko (0)
09.06.2010 12:44
это элементарно конструкция будет стоять, пока центр тяжести будет находиться в контуре основания… та же Пизансакя башня…
kolia78 (0)
31.01.2010 12:17
L/(2 в n-1)
он (10)
08.09.2009 09:42
Если по рисунку, то там, по-моему, уже вторая костяшка подрезала сильно:)) - выступает аж наполовину… "Можно ли собрать такую пирамидку, чтобы проекция на плоскость самой верхней костяшки лежала вне основания самой нижней?" Для этого можно нарастить немного по высоте, выступая совсем по чуть-чуть, а потом уже класть на опору. Если по условию смещение только вправо…
Осьминог (8)
18.07.2009 23:31
главное, чтоб центр масс был справа от наложенной костяшки. но бесконечно много костяшек не выстроить. чтоб конструкция была выше, нужно будет накладывать костяшки друг на друга без сдвига.
Zarathustra (1)
12.05.2009 14:44
Смотрим на центр масс-если не выходит за опору- усе пучком. А а картинке показан неустойчивое положение
SchneeWittchen (1)
24.04.2009 17:11
Ой! В смысле, если не так,как на картинке, а зигзагом!
SchneeWittchen (1)
24.04.2009 17:10
А если так? __ __ __ __ Тогда можно сказать, что длина Л/2 для всех
ИМХО (0)
18.04.2009 10:04
спиралью ложишь…бесконечно долго ))
valentin1976 (-3)
15.04.2009 13:11
Вся конструкция будет устойчива до тех пор,пока,центр тяжести всей конструкции(сколь угодно костяшек) не будет выступать за пределы самой нижней костяшки…(сорри за примитивный ответ)
Ник (1)
12.04.2009 12:59
cheese, Вы правы!
Игорь (2)
10.04.2009 17:12
То ,как нарисовано выше -без клея уже стоять не будет .Домино купите себе.
fantomas (-1)
01.04.2009 18:45
Можно ли собрать такую пирамидку, чтобы проекция на плоскость самой верхней костяшки лежала вне основания самой нижней? НЕЛЬЗЯ мой ответ
Димитрий (23)
29.03.2009 15:51
Значит любая часть доминошек устоит на предыдущей, так как конструкция самоподобна. Осталось заметить, что координата последней доминошки: 1/2+1/4+…+1/(2n-2) = (1+1/2+1/3+…+1/(n-1))*1/2 стремится к бесконечности при увеличении n, так как гармонический ряд (1+1/2+1/3+1/4+… ) расходится. Удивительное рядом!
Димитрий (23)
29.03.2009 15:44
Доказательство моего решения. Вначале покажем, что конструкция будет в равновесии. Докажем, что центр тяжести всех доминошек без первой будет находиться над правым краем первой доминошки для любого n. Координата последней доминошки: 1/2+1/4+…+1/(2n-2). Координата предпоследней: 1/4+1/6+…+1/(2n-2). И т.д. Тогда координата центра масс всей системы без первой доминошки: (1/2+2*1/4+3*1/6+…+(n-1)*1/(2n-2))/(n-1) = ((n-1)*1/2)/(n-1) = 1/2 .
Димитрий (23)
29.03.2009 15:26
Отгадка: чтобы добиться максимального сдвига n-ой доминошки относительно первой надо 2-ую доминошку сдвинуть на 1/(2n-2), 3-ю на 1/(2n-4) относительно предыдущей, четвёртую на 1/(2n-6) и т.д. Последнюю надо сдвинуть на 1/2. Таким образом конструкция устоит, и при достаточно большом n последнюю доминошку можно будет положить сколь угодно правее первой. Проекция УЖЕ ПЯТОЙ доминошки при такой конструкции окажется правее первой на 1/24.
Димитрий (23)
29.03.2009 15:14
Pika и farenheit правы! Но интересен вопрос: как добиться максимального сдвига? Ведь если вторую доминошку положить полевее, то третью можно будет положить поправее. :)
Pika (1)
29.03.2009 01:11
farenheit говорит дело. Нельзя что бы маса от 0 до L была больше чем от L и дальше.В противном случае конструкция рухнет.
Димитрий (23)
28.03.2009 22:16
Мы проходили эту задачку по линейной алгебре. Третью костяшку можно положить со сдвигом 1/4, четвёртую - 1/6, пятую - 1/8 и т.д. Если посчитать, то таким образом центр масс всегда будет на правом краю нижней костяшки. Суммарный сдвиг, которого мы добьёмся равен половине суммы гармонического ряда (1+1/2+1/3+1/4+…), который, как известно, расходится. Значит и в нашем случае мы сможем класть костяшки сколь угодно далеко. В частности уже ПЯТАЯ костяшка будет висеть над полом, а не над первой.
Gennady (1)
28.03.2009 21:08
А кстати да, можно знаете как - придерживая конструкцию, класть доминошки с уклоном влево, т.е. чтобы она перевешевила в левую сторону, а потом вправо начать строить, чтобы проекция последней лежала вне нижней =) Получится, что она не упадет, т.к. центр масс придется по центру, но чит в том, что ее нужно придерживать при строении) хз прокатит или нет такое решение =)
Sum (-1)
28.03.2009 18:06
Я считаю, можно, если делать "ветви" из костяшек не только в одну сторону что-то вроде перевёрнутой пирамиды, где аоверх "ветви" ложется "серединная" костяшка уравновешивает центр тяжести всей конструкции.
farenheit (4)
27.03.2009 16:52
Если вторая доминошка лежит со сдвигом L/2, как в задаче, то третью можно класть только ровно на вторую, без сдвига, иначе центр тяжести совокупности 2-й и 3-й костяшки будет уже за краем первой. Если вторую класть со сдвигом L/(x
R0mka (18)
27.03.2009 05:28
Чтобы конструкция не падала надо Третью и последующии ложить на растояние менее L/2 КАЖДОЙ уже лежащей доминошки. Поэтому нельзя построить даже такую пирамиду где больше половины верхней доминошки была бы вне основания первой.
Каретный (9)
27.03.2009 01:35
Нет, нельзя. У нас получился предел, в котором проекция левой стороны верхней костяшки бесконечно стремится к правой стороне нижней костяшки.
cнeese (5)
26.03.2009 18:10
центр тяжести самой верхней всегда должен быть над основанием первой, dixi.
genix (0)
26.03.2009 17:35
ИМХО чтоб понять упадет конструкция или нет, надо от края нижней доминошки (допустим, правого, как на рисунке) провести вверх воображаемую черту (прямо до сферического коня) ну и если справа масса всего этого будет больше, чем суммарная масса всех обрезков, которые слева, то все повалится к чертям =)
Darina_ (2)
26.03.2009 13:16
Ну если только первую не с середины положить, а ближе к левому краю, наверное можно, где то штук 6 потребуется… А может вообще не получиться.
RR (1)
26.03.2009 12:45
ну наверно можно где то с 7-й костяшки